New Designs for School
The Anatomy of a Math Skill
New Classrooms Team
in New York, NY
Topics
We’ve all had the experience of truly purposeful, authentic learning and know how valuable it is. Educators are taking the best of what we know about learning, student support, effective instruction, and interpersonal skill-building to completely reimagine schools so that students experience that kind of purposeful learning all day, every day.
By breaking down math skills into procedural, conceptual, and applied understanding, we can better see the connections between skills and what it takes for students to authentically learn them.
What do we mean when we talk about learning new “skills” in the context of mathematics? At its simplest form, a skill means the ability to do something well, according to the Oxford dictionary. Yet the term “skill” has often invoked negative connotations in traditional K-12 academic settings for being synonymous with lower-level learning.
At Teach to One, when we refer to a skill, we mean the procedural, conceptual, and applied knowledge of skill. And due to the cumulative nature of math, students simply can't acquire meaningful knowledge if it isn’t undergirded by a series of specific and interconnected skills they learn over time.
Teach to One’s Major Concept Map visually illustrates the relationships between 64 prioritized mathematical concepts, which are made up of 206 discrete core skills and 37 enrichment skills, that students generally learn from 5th grade through algebra. (It also outlines 23 non-prioritized concepts and their 100 related skills—though these are not critical for algebra readiness.) Each of the prioritized concepts enables deep thinking about big ideas and core content. The visual connections between the concepts allow teachers and students to examine the interrelated nature of mathematics and how a student’s year-long learning plan can be shaped.
For more than a decade, our team of academic experts, curriculum developers, and technologists have been obsessed with understanding, at precise levels, the connections between mathematical skills and what it takes for students to authentically learn them. Let’s explore the anatomy of a skill and study skills under a microscope–through the lens of precision learning.
Anatomy of a Math Skill: Procedural, Conceptual, & Applied Understanding
Education publishers and teachers who create their own curricula have the critical role of converting grade-level standards into a teachable lesson. Many standards incorporate multiple skills, each of which generally requires its own lesson. And moreover, in order to learn these new skills, predecessor knowledge is often required.
Although some lessons may focus on discrete skills at varying levels of depth, teachers must also integrate lessons that enable students to explore their connections to one another, to broader mathematical ideas, and to the world more generally.
We can break down the complex nature of math skill progressions into the procedural, conceptual, and applied dimensions of understanding.
Procedural Understanding
One aspect of skill mastery is gaining procedural understanding. This level of understanding involves knowing how to perform a specific task in which context is provided. The knowledge of how to complete the task would only encompass discrete facts and individual processes. For example, a student may be asked specifically to find the hypotenuse of a triangle.
Conceptual Understanding
A second level of skill mastery is conceptual understanding. Beyond knowing how to find an answer, which is the procedural part of the skill, conceptual understanding means understanding why a procedure works as it does, why it is important, and when it should be used. A student with conceptual understanding of the Pythagorean Theorem will understand why the relationship among the side lengths exists, when it applies, and how to use it to find the information they need.
Applied Understanding
Applied understanding proves procedural and conceptual understanding. The knowledge of when to use a certain skill unites with the knowledge of how to complete that specific task in applied understanding. Successfully using a mathematical concept or procedure to solve a problem is one example of demonstrating applied understanding.
Precision Learning: Knowing Where Students Are in Order to Get Them to Where They Need to Be
Nationally, student proficiency on the 8th grade National Assessment of Education Progress (NAEP) is six points lower than what it was on the 4th grade NAEP four years prior. That same pattern of students falling behind holds true in every U.S. state, a trend which does not hold true for reading.
We believe a key reason for this phenomenon has to do with the fact that student instruction is oriented around grade-level math standards even though students may be missing many of the key foundational elements, or skills, required to master them. Students who fall behind need a viable path to catch up, but schools’ orientation around grade-level instruction makes addressing those gaps far more difficult. We wrote extensively about this in The Iceberg Problem.
Solving this dilemma requires tailored acceleration一academic bridges that meet students where they are and connects them to where they need to be.
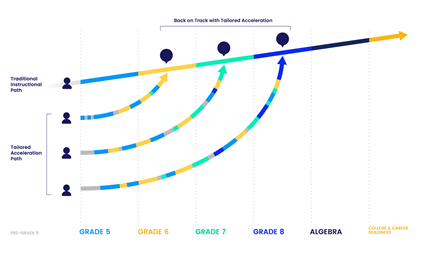
That academic bridge starts with understanding precisely what skills a student knows (procedurally, conceptually, and applied). Then each student requires a personalized mix of pre-, on-, and post-grade skills aligned to their specific strengths and needs with the goal of catching up and moving ahead.
Without this type of precision learning, gaps in understanding fundamental skills procedurally, conceptually, and in application compound and make learning more difficult for the student, as well as making the teacher’s job more challenging.
Bringing Precision Learning to Math Classrooms
With Roadmaps, Teach to One provides a free adaptive diagnostic assessment in math for grades four through algebra to understand the precise pre-, on-, and post-grade skills students need to achieve proficiency. Then, students, teachers, and even families can access instructional tools and high-quality, curated content from multiple providers aligned to each student’s individualized roadmap to support them in the classroom and at home. You can learn more about this digital learning solution by visiting www.teachtoone.org.
In order to get students where they need to be, educators need to know precisely where students are starting. Identifying the skills students know (pre-, on-, and post-grade) and the depth in which they understand these skills (procedural, conceptual, and applied knowledge) is critical to giving students a pathway to catch up or get ahead.
All images courtesy of New Classrooms Innovation Partners.
New Classrooms Team
New Classrooms Innovation Partners, a nonprofit organization, has been working for over a decade with middle schools to implement and iterate on a comprehensive middle school math program to effectively address the problem of learning loss. A cross-functional team of policy, academic, and curriculum experts contributes to the development and publication of its policy white papers.
